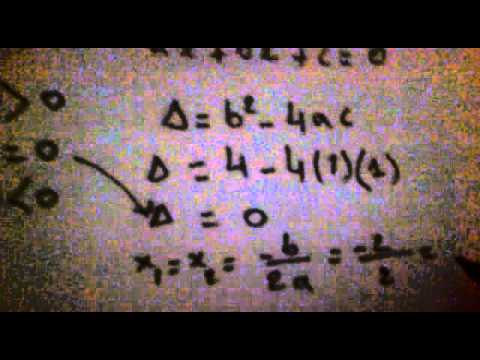حل معادلة من الدرجة الثانية دلتا

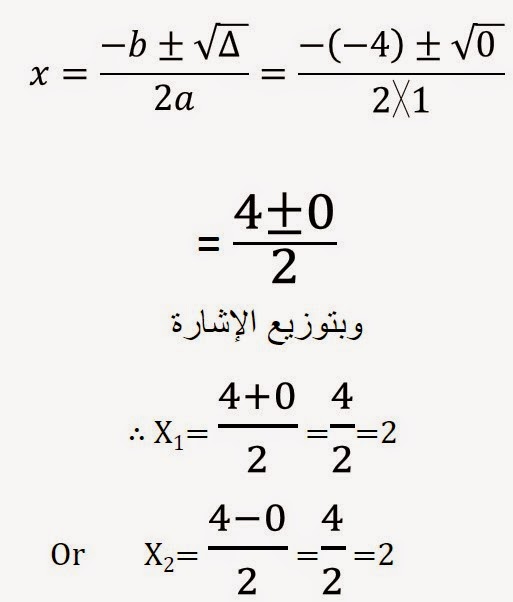
حل معادلات الدرجة الثانية في متغير واحد بطريقة القانون العام تصادفنا الكثير من المعادلات التي يصعب حلها باستخدام التحليل وقد تأخذ منا وقتا أطول من اللازم في حلها بإكمال المربع مثل المعادلة.

حل معادلة من الدرجة الثانية دلتا. حل معادله درجه دوم به روش دلتا. حل معادلة من الدرجة الثانية وتعرف المميز delta lang l. در اینجا سه حالت پیش می آید. يسمى الحرف الرابع من الأبجدية اليونانية دلتا في العلم بالتغيير في أي قيمة أو خطأ أو زيادة.

المميز دلتا نستعمل المميز دلتا في حل المعادلات والمتراجحات من الدرجة الثانية من الشكل التالي ax bx c 0 حيث أن a b c هي معاملات ولكي يتم حساب المميز دلتا يجب تطبيق القانون التالي δ b 4 a c. اذا كان المميز موجب فللمعادلة حلين اذا كان يساوي صفر حل واحد اذا كان سالبا ليس للمعادلة اي. يمكن حل المعادلة من الدرجة الثانية بمجهول واحد أو المعادلة التربيعية بعدة طرق منها التعميل أو التحليل إلى عوامل جداء ومنها طريقة إكمال المربع الكامل وطريقة الصيغة التربعية أو المميز طريقة دلتا delta ثم طريقة الحل. توجد عدة طرق لحل المعادلة من الدرجة الثانية لكن في هذا الدرس سوف نركزعلى كيفية حل المعادلة من الدرجة الثانية بإستعمال المميز دلتا 𝞓 أما الطريقة الثانية التي سوف نتحدث عنا هي طريقة المقص.

با فرض داشتن معادله درجه دوم به شکل برای حل معادله به روش دلتا باید مراحل زیر را طی کنیم.